von Alexander Graham Bell (Präsident der National Geographic Society)
|
Im Jahre 1899, während unserer Akadamie-Versammlung im April, hielt ich einen Vortrag über das Thema: "Drachen mit radialen Flügeln"; einige der dort vorgestellten Illustrationen wurden dann hinterher auch im Monthly Wheather Review veröffentlicht. Seit dieser Zeit habe ich mich sehr intensiv mit Drachenexperimenten beschäftigt. Warum, weiß ich selbst nicht genau, vielleicht wegen der engen Beziehung zur Flugmaschinenproblematik. Jeder von uns sind an Luftfahrt interessiert, und ich bin ziemlich sicher, daß niemand, der aufmerksam den Flug der Vögel verfolgt, Zweifel daran hat, daß ein Flug von Gebilden schwerer als Luft möglich ist. Oder mit den Worten einen alten Gelehrten ausgedrückt: "Wir können nicht etwas bezweifeln, was schon längst vollbracht ist." Ich war der Überzeugung, daß eine richtig konstruierte Flugmaschine auch als Fessel-Drachen geflogen werden können müßte, und umgekehrt, ein richtig konstruierter Drachen auch als Flugmaschine benutzt werden könnte, sofern er einen eigenen Antrieb besäße. Allerdings bin ich von der Richtigkeit der ersteren Behauptung nicht ganz so überzeugt wie von der letzteren. Nehmen wir einen Drachen mit einer als Flugmaschine geeigneter Form, der so effizient ist, daß er in einer guten Brise (sagen wir mal 9 m/s) fliegt, wenn er mit Gewicht entsprechend Pilot und Motor belastet wird, dann müßte eigentlich der selbe Drachen mit einem richtigen Piloten und richtigem Antrieb 9 m/s in ruhigem Wind als Flugmaschine funktionieren. Solange man den Luftdruck beachtet, ist es sicherlich unerheblich, ob sich die Luft gegenüber dem Drachen bewegt, oder aber der Drachen gegenüber der Luft. In anderer Hinsicht sind diese beiden Fälle natürlich nicht gleich. Ein Drachen, der in einer 9 m/s- Brise fliegt, besitzt keinen Impuls, bzw. die Summe aller an ihm wirkenden Kräfte ist gleich Null, da er in der Luft steht und keine Eigenbewegung hat. Hingegen ist die Impulsgröße einer mit 9 m/s angetriebenen Flugmaschine ziemlich beträchtlich. Dieser Impuls unterstützt sicherlich den Flug und ist sogar wahrscheinlich sehr hilfreich, um die Schwerkraft unabhängig vom Luftdruck zu überwinden. Es ist deshalb absolut denkbar, daß ein Apparat, der seine Fähigkeiten als Flugmaschine unter Beweis gestellt hat, wegen des fehlenden Antriebes nicht als Drachen geflogen werden kann. Wie auch immer, die Übertragbarkeit von Drachenexperimenten auf das Flugmaschinenproblem ist für eine lange Zeit ein Leitgedanke in meinen Überlegungen gewesen. Ich habe mich nie darum gekümmert, wie hoch man einen Drachen fliegen könnte oder einen Drachen zu bauen, der besonders hoch fliegt. Der Punkt, auf den ich mich konzentrierte, war folgender: Die Stabilität der Drachenstruktur sollte in der Luft perfekt sein; der Drachen sollte zuverlässig fliegen und nicht hin und her schaukeln oder gar kopfüber abstürzen, wenn er von einer plötzlichen Böe getroffen wird. Wenn die Leine losgelassen wird, sollte er ruhig und sanft ohne Materialschwingungen zur Erde gleiten. Außerdem habe ich noch festgestellt, daß es wichtig ist, daß das Gestänge möglichst stark und leicht ist. Ich glaube, daß in der nun gefundenen Form der Drachenstruktur die Eigenschaften von Stärke, wenig Gewicht und zuverlässigem Flug in einem bemerkenswertem Maß vereinigt worden sind. In meinen jungen Jahren verband man mit dem Wort "Drachen" eine kreuzförmige und mit Papier bespannte Holzstruktur, die eine diamantartige Oberfläche bildete, der Längsschenkel länger als die Spreize, zusätzlich mit einem langen Schwanz, bestehend aus einer Schnur, an der in regelmäßigen Abständen Papierstückchen befestigt waren. Solch ein Drachen ist einfach nur ein Spielzeug. In Europa und Amerika, wo dieser Drachentyp vorherrscht, wurde Drachensteigen nur als Zeitvertreib für Kinder angesehen, und Verbesserungen der Form der Drachenstruktur kaum als geeignetes Objekt für wissenschaftliche Überlegungen in Erwägung gezogen. In Asien ist Drachensteigen jahrhundertelang ein Freizeitvergnügen für Erwachsene gewesen; in China, Japan und auf den malayischen Inseln wurden schwanzlose Drachen entwickelt, die bis vor kurzen jeder uns bekannten Drachenform weit überlegen waren. Erst in den letzten Jahren wurde bei uns ernsthaft über Verbesserungen an Drachenstrukturen nachgedacht. Vor allem einem Mann habe wir diese Entwicklungen in der letzten Zeit zu verdanken: Laurence Hargarve aus Australien. Hargrave erkannte, daß eine Struktur, die zu einem guten Drachen führt, ebenso Grundlage für die Entwicklung einer Flugmaschine sein könnte. Seine Forschungsergebnisse, die von der Royal Society of New South Wales veröffentlicht wurden, sind weltbekannt und bilden in Europa und Amerika die Grundlage für moderne Forschungen auf diesem Gebiet. Alles, was mit Luftfahrt zu tun hat, erregt allgemeines Interesse und auch der wissenschaftliche Drachenflug ist durch Hargraves Experimente angeregt worden. In Amerika allerdings war der Hauptantriebsgrund für wissenschaftliches Drachensteigen die vom US Weather Bureau gewonnene Erkenntnis, daß man wichtige Wetterinformationen erhalten könne, wenn man mit geeigneten Drachen meteorologische Instrumente in große Höhen verbringen könnte. Mr. Eddy und andere haben den schwanzlosen Malay-Drachen als Grundlage für ihre Experimente benutzt, während Professor Marvin vom US Weather Bureau und Mr. Rotch vom Blue-Hill Observatorium und viele andere den Kastendrachen von Hargrave für diesen Zweck gewählt haben. Die Regierung hatte sich die Unterstützung des Weather Bureaus bei den Drachenexeperimenten zu eigen gemacht, und so vor einigen Jahren mit Marvin-Drachen ausgerüstete Wetterstationen überall in den Vereinigten Staaten eingerichtet. Am Blue-Hill-Observatorium in Massachusetts wurden regelmäßigen Wettermessungen in großer Höhe gemacht, und Mr. Rotch hat bewiesen, daß es möglich ist, Drachen an Dampfschiffen zu führen und so quer über den Atlantik eine kontinuierliche Reihe von Messungen zu gewährleisten. |
Hargrave hat die zellulare Bauweise von Drachen eingeführt. Er baute Drachen, die aus verschiedenen Zellen zusammengesetzt waren, fand aber keinen Vorteil durch Verwendung von mehr als zwei Zellen heraus. So ist dann auch ein Drachen, bestehend aus zwei durch einen großen Zwischenraum getrennten rechteckigen Zellen allgemein als "Hargrave-Kastendrachen" bekannt geworden. Dieser stellt für mich den Höhepunkt des Fortschritts im 19. Jahrhundert dar und war Ausgangspunkt für meine eigenen Forschungen (Fig.1).
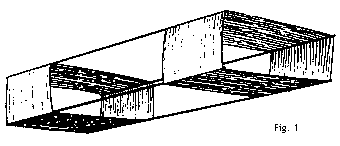 Die vordere und hintere Zelle sind durch ein Gestänge in der Weise verbunden, daß ein großer Zwischenraum zwischen ihnen verbleibt. Dieser Zwischenraum ist ein wesentliches Merkmal dieses Drachens; von ihm hängen vordere und hintere Stabilität des Drachens ab. Je größer der Zwischenraum, desto stabiler ist das Gleichgewicht des Drachen in Längsrichtung, desto leichter nimmt er eine horizontale Position in der Luft ein und desto weniger neigt er dazu, kopfüber abzustürzen oder wie ein Schiff in rauher See zu stampfen. Stampfbewegungen oder Schwingungen werden fast vollständig unterdrückt, wenn der Zwischenraum zwischen beiden Zellen entsprechend groß ist. Jede Zelle verfügt über vertikale Flächen, die wiederum ein wesentlicher Bestandteil des Drachens für seine seitliche Stabilität sind. Je größer die vertikalen Flächen, desto größer ist die Seitenstabilität und um so weniger tendiert der Drachen zu seitlichen Bewegungen oder Drehungen in der Luft. In der obenstehenden Beschreibung habe ich nur die absolut notwendigen Teile der Konstruktion beschrieben, mit gerade genug Gestänge, um die Zellen zusammen zuhalten. Es ist klar, daß ein Drachen, wenn er so wie in Fig.1 konstruiert ist, eine ziemliche wacklige Angelegenheit ist. Man benötigt verschiedene zusätzliche Versteifungen unterschiedlicher Art, damit die Drachenflächen ihre Stellung zum Wind behalten und um Verziehen, Verdrehen und sonstige Störungen der Form im Winddruck zu vermeiden. Unglücklicherweise verringern die nötigen Zusatzversteifungen den Wirkungsgrad des Drachens: Einerseits wird das Verhältnis Gewicht zu Fläche größer, andererseits wird der Luftwiderstand vergrößert. Die inneren Versteifungen liegen im Luftstrom, tragen also zur Richtungsstabilität bei, ohne aber gleichzeitig für zusätzlichen Auftrieb zu sorgen.  Eine rechteckige Zelle ähnlich Fig.2 hat prinzipbedingt eine schwache Struktur, da man sie beispielsweise mühelos ohne großen Kraftaufwand in die Form B bringen kann. Um diese Verzerrungen zu vermeiden, ist es empfehlenswert, innere Versteifungen wie in C vorzusehen. Diese inneren Versteifungen, selbst wenn sie aus feinstem Draht hergestellt sind, erhöhen Gewicht und Luftwiderstand, ohne selbst aerodynamische Vorteile zu bringen. |
|
Wenn ich über die Reihe meiner eigenen Experimente zurückblicke, muß ich sagen, daß die Einführung von Dreieckzellen ein echter Fortschritt war, einer der Punkte, die sich vor dem Nebel unzähliger Detaillösungen klar herausgestellt haben. Nachfolgend (Fig.3) eine Beschreibung eines typischen Drachens aus Dreieckzellen, der nach dem selben Hargrave-Prinzip wie in Fig.1 aufgebaut ist. 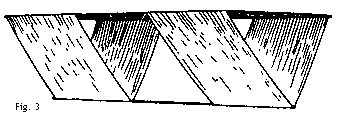 Ein Dreieck ist durch seine Struktur perfekt in seiner eigenen Ebene stabilisiert, und daher sind in einem Drachen mit Dreieckzellen (siehe Fig.3) innere Versteifungen, um Verzerrungen ähnlich wie beim Hargrave-Drachen (Fig.2) anfangs beschrieben zu vermeiden, absolut unnötig.
Ein Dreieck ist durch seine Struktur perfekt in seiner eigenen Ebene stabilisiert, und daher sind in einem Drachen mit Dreieckzellen (siehe Fig.3) innere Versteifungen, um Verzerrungen ähnlich wie beim Hargrave-Drachen (Fig.2) anfangs beschrieben zu vermeiden, absolut unnötig.Der Auftrieb solch einer Dreieckszelle ist zwar vielleicht geringer als bei einer Rechteckzelle, aber der enorme Zuwachs an struktureller Stärke, verbunden mit der Verringerung des Luftwiderstandes und Gesamtgewichts, gleicht eventuelle Nachteile in diesem Bereich aus. Die horizontalen Flächen eines Drachens sind diejenigen, die den durch die Schwerkraft bedingten Abstieg verhindern, während die vertikalen Flächen verhindern, daß sich der Drachen in der Luft dreht. Schräge Flächen lassen sich bequem in vertikale und horizontale Komponenten zerlegen, d.h. in Auftrieb erzeugende und stabilisierende Flächen. 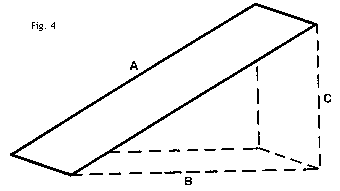 Die schräge Drachenfläche A (Fig.4) zum Beispiel kann als funktionell gleichwertig wie die beiden Flächen B und C angenommen werden. Allerdings ist das Material, aus dem die Fläche A gebildet wird, im Vergleich zu den Flächen B und C fast gewichtslos, und das Gestänge zur Versteifung von A wiegt weniger als die Versteifungen für B und C.
Die schräge Drachenfläche A (Fig.4) zum Beispiel kann als funktionell gleichwertig wie die beiden Flächen B und C angenommen werden. Allerdings ist das Material, aus dem die Fläche A gebildet wird, im Vergleich zu den Flächen B und C fast gewichtslos, und das Gestänge zur Versteifung von A wiegt weniger als die Versteifungen für B und C.In der Dreieckszelle in Fig.5 sind die schrägen Flächen ab und bc funktionell gleichwertig wie die drei Flächen ad, de und ec, aber viel leichter. Die schrägen Flächen haben hier also Vorteile. 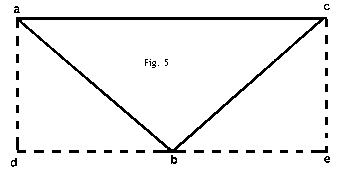 Der einzige Nachteil der ganzen Konstruktion besteht darin, daß die Luft bei der Dreiecksvariante nicht so ungehindert wie bei der Rechteckvariante die Fläche ac beströmen kann, so daß hier der Wirkungsgrad nicht ganz so gut ist. Während also in der Theorie die Dreieckszelle im Vergleich zu Hargrave's Rechteckzelle auftriebsmäßig leicht unterlegen ist, ist in der Praxis kaum ein Unterschied feststellbar. So weit ich das in meinen Versuchen beobachten konnte, scheint ein Drachen, der nach demselben Konstruktionsprinzip aufgebaut wie der Hargrave, aber mit Dreieckzellen ausgestattet ist, genauso gut und mit demselben Flugwinkel wie ein normaler Hargrave zu fliegen. Solche Drachen sind daher besser, denn sie fliegen genauso gut, sind aber stabiler, leichter und haben einen kleineren Luftwiderstand. Dreieckzellen sind also zur Kombination in einer Verbundstruktur, in welcher sich die Drachenflächen sich nicht gegenseitig stören, wunderbar geeignet. Zum Beispiel formen drei Dreieckszellen-Drachen, die an den Ecken verbunden sind, einen sehr gut fliegenden Verbunddrachen (Fig.6). 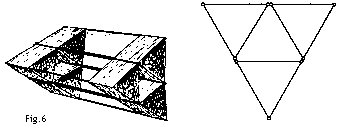 Das Gewicht dieses Verbunddrachens ist die Summe des Gewichts aus den drei Einzeldrachen, und die resultierende Gesamtfläche ist die Summe der Fläche der Einzeldrachen. Das Flächengewicht des Verbunddrachens ist also das gleiche wie in den verbundenen Einzeldrachen. Es ist klar, daß in solchen Verbunddrachen die Verdopplung der Längsstäbe, da wo die Ecken verbunden werden, eigentlich überflüssig ist, da es einfach ist, diesen Drachen so zu konstruieren, daß nur ein Stab anstelle der Doppelstäbe verwendet wird. |
Beispiel: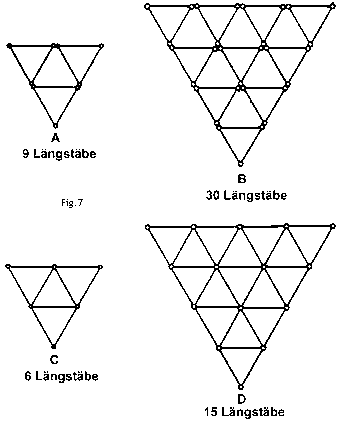 Die Verbunddrachen A und B (Fig.7) können so konstruiert werden wie in C und D, mit dem Vorteil, daß das Gesamtgewicht ohne Stabilitätsverlust reduziert werden kann. In diesem Fall ist das Gesamtgewicht des Verbunddrachens bei gleicher Fläche kleiner als das der Einzeldrachen.
Die Verbunddrachen A und B (Fig.7) können so konstruiert werden wie in C und D, mit dem Vorteil, daß das Gesamtgewicht ohne Stabilitätsverlust reduziert werden kann. In diesem Fall ist das Gesamtgewicht des Verbunddrachens bei gleicher Fläche kleiner als das der Einzeldrachen.Wenn man unendlich viel Drachen auf diese Art miteinander verbinden könnte, hätten wir das kuriose Resultat, daß sich das Flächengewicht des Drachens mit jeder Vergrößerung verringern würde. Unglücklicherweise benötigt der Drachen für einen stabilen Flug einen bestimmten Raum zwischen Vorder- und Hinterzelle (Fig.6); und wenn wir den Durchmesser unserer Verbundstruktur vergrößern ohne gleichzeitig den Raum zwischen den Zellen zu verlängern, vermindern wir die Flugeigenschaften unseres Drachens. Jedes Vergrößern des Abstandes zwischen Vorder- und Hinterzelle bedingt nämlich eine Zuwachs an "leerem" Gestänge und führt daher zu Gewichtszunahme und Vergrößern des Flächengewichts. Während Drachen mit Dreieckszellen stabil in tranversaler (seitlicher) Richtung sind, sind sie in Longitudinalrichtung (von vorne nach hinten) strukturell schwach, da in dieser Richtung die Drachenstruktur rechteckig ist. 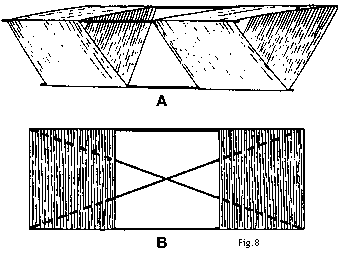 Jede Seite des Drachens A (Fig.8) beispielsweise erfordert diagonale Spreizen in der Art wie in B gezeigt, um durch Winddruck bedingte Strukturverzerrungen zu vermeiden. Die notwendigen Spreizen vergrößern allerdings nicht den Luftwiderstand, da sie nicht im Luftstrom liegen, sondern vergrößern nur das Flächengewicht durch Zufügung von toter Last. |
Nachdem ich nun in aller Stille eine Vielzahl von Drachenkonstruktionen in meinem Laboratorium in Nova Scotia untersucht habe, komme ich zu einem weiteren wichtigen Punkt - einem anderen Meilenstein des Fortschritts - nämlich zur Verwendung von Dreieckszellen in jeder Richtung (longitudinal und transversal), und der ganz klaren Wichtigkeit der Struktur der vierflächigen Pyramide, speziell der gleichseitigen, als Strukturelement für Drachen und Flugmaschinen.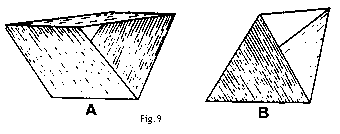 Stellen wir uns den Fall einer normalen Dreieckszelle A (Fig.9) vor, deren Querschnitt lateral dreieckig, aber longitudinal quadratisch ist. Wenn wir nun den longitudinalen ebenso wie den transversalen Querschnitt dreieckig machen, kommen wir zu einer Zellenform wie in B, in der das Außengestell eine vierseitige Pyramide bildet. In diesem Fall sind die Flächen dreieckig und die ganze Konstruktion erinnert stark an ein paar angewinkelte Vogelflügel, die über die Spitzen mit einer Spreize verbunden sind (siehe B, Fig.9, ebenso wie die Zeichnungen der Tetra-Zellen in Fig.10). 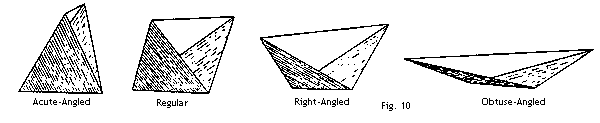 Ein Tetraeder ist ein Körper, der von vier Dreiecksflächen begrenzt wird. Ein gleichmäßiger Tetraeder besteht aus vier gleichseitigen Dreiecken und sechs gleichlangen Seiten. Im Drahtmodell sind nur die Kanten sichtbar, und das Drahtmodell eines Tetraeders kann aus sechs gleichlangen Stäben gebidlet werden, die an den Ecken so verbunden werden, daß sie vier gleichseitige Dreiecke bilden. Die meisten von uns kennen das Puzzle, wie man vier Dreiecke aus sechs Streichhölzern bildet. Gib einem Bekannten sechs Streichhölzer und bitte ihn, daraus vier gleichseitige Dreiecke zu bilden. Die Schwierigkeit liegt in der unbewußten Annahme des Probanden, daß alle vier Dreiecke in der gleichen Ebene liegen müßen. In dem Augenblick, in dem er erkennt, daß diese nicht alle in in der gleichen Ebene liegen müßen, ist die Lösung des Problems leicht. Drei Streichhölzer werden als Dreieck auf den Tisch gelegt, die anderen drei werden wie ein Dreibein auf die Ecken gestellt. Die Streichhölzer formen das Skelett eines gleichseitigen Tetraeders (Fig. 11). 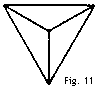 Ein Rahmen, der nach diesem Modell der sechs an den Enden verbundenen Stäbe geformt ist, bildet eine Tetraederzelle, die die Eigenschaften von Stabilität und wenig Gewicht in hohem Maße besitzt. Es ist nicht nur in zwei räumlichen Richtungen wie ein Dreieck abgespreizt, sondern in drei wie ein Körper. Es besitzt "dreidimensionale" Stärke und nicht "zweidimensionale" Stärke wie ein Dreieck oder "eindimensionale" Stärke wie ein Stab. Es ist das Gerüst eines Körpers, und nicht das einer Fläche oder Linie. |
|
Es ist erstaunlich, wie stabil so ein Gerüst ist, selbst wenn man es aus sehr leichtem und zerbrechlichem Material bildet; und Verbundstrukturen, die durch Eckenverbindungen verschiedener Tetraeder wieder ein größeres Tetraeder formen, besitzen die gleiche Stabilität. Fig.12 zeigt eine aus vier Gerüsten wie in Fig.11 gebildete Struktur, und Fig.13a eine aus vier Gerüsten wie in Fig.12 gebildete Struktur. 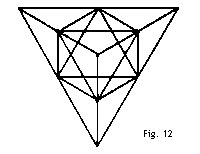 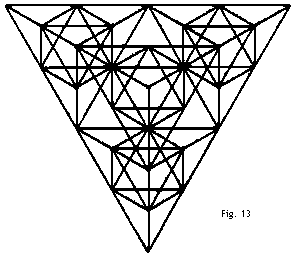 Wenn man ein Tetraedergerüst mit Seide oder anderen geeigneten Stoffen bespannt, wird es ein Tetraeder-Drachen, bzw. der Drachen hat die Form eines Tetraeders. 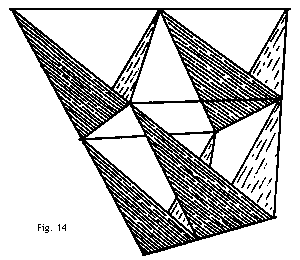 Der Drachen in Fig.14 wird aus vier geflügelten gleichseitigen, an den Ecken verbundenen Tetraedern (siehe Fig.10) gebildet. Vier von den Drachen aus Fig.14 wiederum werden in gleicher Weise kombiniert (Fig.15), und vier Drachen wie in Fig.15 werden wie in Fig.16 D verbunden. 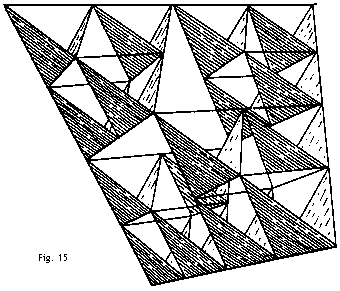 Bei dieser Konstruktionsart bleibt in der Mitte des Drachens ein achtflächiger leerer Raum übrig, der dieselbe Funktion wie der Raum zwischen den beiden Hargrave-Zellen zu haben scheint. Die Tetraeder-Drachen, die den größten Raum in der Mitte frei haben, können am besten ihr Gleichgewicht in der Luft halten. Der beste Platz, um die Flugleine zu befestigen, ist das äußerste Ende des Bugs. Wenn die Flugleine weiter weg vom Kiel befestigt wird, bildet die Flugleiner einen immer größer werdenden Winkel mit dem Horizont und der Drachen fliegt fast überkopf; es ist aber nicht ratsam, den Anleinpunkt weiter als bis zur Mitte des Kiels zusetzen.  Eine gute Stelle für hohe Flüge ist ein Anleinpunkt in der Mitte zwischen Bug und der Mitte des Kiels.
Bei den Tetraeder-Drachen in Fig.16 hat die Verbundstruktur selbst in jedem Fall die Form eines gleichseitigen Tetraeders, und daher gibt es keinen Grund, dieses Kombinationsprinzip endlos weiter bis zu sehr großen Kombinationen zu verfolgen. Das Flächengewicht bleibt dasselbe, egal wie groß der Verbunddrachen sein mag.
Eine gute Stelle für hohe Flüge ist ein Anleinpunkt in der Mitte zwischen Bug und der Mitte des Kiels.
Bei den Tetraeder-Drachen in Fig.16 hat die Verbundstruktur selbst in jedem Fall die Form eines gleichseitigen Tetraeders, und daher gibt es keinen Grund, dieses Kombinationsprinzip endlos weiter bis zu sehr großen Kombinationen zu verfolgen. Das Flächengewicht bleibt dasselbe, egal wie groß der Verbunddrachen sein mag.Der Vierzellen-Drachen B wiegt beispielsweise viermal so viel wie eine Zelle und hat eine vierfache Fläche, der Sechzehnzeller in C hat sechszehn Mal soviel Gewicht und Fläche und der Vierundsechzigzeller hat vierundsechzig Mal soviel Gewicht und Fläche. Das Flächengewicht ist das gleiche für kleine und große Drachen. Auf den ersten Blick scheint dies mit gewissen mathematischen Folgerungen unvereinbar, die Prof. Simon Newcomb in einem Artikel "Kommt das Luftschiff ?" in McLure's Magazin Sept. 1901 veröffentlicht hat. Diese Folgerungen führten ihn zu der Überzeugung, daß "die Konstruktion eines Luftfahrzeuges, das in der Lage wäre, einen Menschen zu seinem eigenen Vergnügen von einem Ort zum anderen zu befördern, die Entdeckung eines neues Materials oder einer neuen Kraft erfordert." Die Überlegungen, die Prof. Newcomb zu diesem bemerkenswertem Resultat geführt hatten, sind ohne Zweifel richtig. Seine Folgerung jedoch läßt noch Fragen offen, da er eine allgemeine Folgerung aus begrenzten Vorgaben gezogen hat. |
|
Er sagt: "Stellen wir uns zwei Flugmaschinen vor, beide exakt gleich, die eine aber in genau doppelt so großen Abmessungen. Wir wissen, daß Volumen und damit Gewicht von zwei ähnlichen Körpern proportional sind. Zwei hoch drei sind acht; daher wird die große Maschine achtmal so viel wiegen wie die kleine. Aber Flächen sind nur die Quadrate der Dimensionen. Zwei zum Quadrat ist vier. Die schwerere Maschine wird also nur die vierfache Fläche der kleineren besitzen und somit ein schlechteres Flächengewicht."
Prof. Newcomb zeigt hier, daß wenn zwei Flugmaschinen (oder Drachen in diesem Fall) exakt gleich sind und sich nur im Verhältnis ihrer Abmessungen unterscheiden, daß das Flächengewicht bei der größeren Maschine größer ist als bei der kleinen, und weiter mit jeder Vergrößerung ansteigt. Daraus folgert er, daß wenn wir unser Luftfahrzeug groß genug machen, wird es zu schwer zum Fliegen sein. Das ist sicherlich soweit richtig und es begründet meine Fehlversuche, einen riesigen menschentragenden Drachen auf Basis der Hargrave-Drachen zu konstruieren. Wenn man solch einen Drachen konstruiert, jede Zelle so groß wie ein kleines Zimmer, braucht man einen Hurrikan, um diesen Drachen abheben zu lassen. Der Drachen war nicht nur nicht in Lage, eine menschenähnliche Last zu tragen, er war noch nicht einmal in der Lage, sich selbst in einer gewöhnlichen Brise, in der kleinere Drachen des gleichen Modells perfekt flogen, anzuheben. Ich habe keinen Zweifel, daß andere Forscher ebenfalls den Fehler gemacht haben, zu vermuten, große Strukturen würden notwendigerweise flugtauglich sein, da ja kleinere Strukturen ihre Flugtauglichkeit schon bewiesen haben. Prof. Newcomb klare Feststellung der zweifelhaften Natur dieser Annahme ist sicherlich eine wichtige Erkenntnis für alle Forscher. Doch Prof. Newcomb's Ergebnisse sind wahrscheinlich nur unter seinen Vorgaben richtig. Für zwei exakt gleiche Modelle, die sich nur in der Größe ihrer Dimensionierung unterscheiden, sind seine Ergebnisse unzweifelhaft richtig; aber sobald große Drachen aus einer Anzahl von kleinen Drachen zu einer Zellstruktur zusammengefaßt werden, liegen die Verhältnisse anders. Meine eigenen Versuche mit Verbunddrachen, die aus an den Ecken verbundenen Dreieckzellen zusammengesetzt werden, haben gezeigt, daß solch ein Drachen zu einer erheblichen Größe kombiniert werden kann, ohne das Flächengewicht zu verändern; bei dem Tetraeder-Plan von Fig.16 bleibt das Flächengewicht gleich, egal wie groß der Verbunddrachen auch sein mag. Die unendliche Vergrößerung dieser Dreieckskonstruktion wird allein durch den Fakt begrenzt, daß das "tote" Gewicht in Form des leeren Rahmens im Zentralraum zwischen den Zellen aus Stabilitätsgründen notwendig ist (siehe Fig.6), so daß die notwendige Vergrößerung dieses Raumes bei der Vergrößerung des Verbunddrachens auch mehr "totes" Gewicht hinzufügt. |
|
Bei den Tetraeder-Drachen in Fig.14,15 und 16 ist dieser Raum nicht notwendig, da durch die Art der Konstruktion auch ohne diesen Raum Stabilität gegeben ist. Tetraeder-Drachen vereinen in hohem Maße Stärke, wenig Gewicht und stabilen Flug; aber es sind noch weitere Experimente erforderlich um herauszubekommen, ob diese Form die ideale Form für einen Drachen ist, oder ob geflügelte Zellen ohne horizontale Tragflächen die beste Tragflächenform darstellen. Das Tetraeder-Prinzip erlaubt uns die Konstruktion von stabilen Strukturen aus leichtem Rahmenwerk in jeder gewünschten Form, und die daraus entstandenen Strukturen sind hervorragend für die Verwendung als Tragflächen in jeder gewünschten Form und Größe geeignet (gerade oder profilierte Tragflächen, groß oder klein, usw.). Als zusätzliche Illustration der Tetraeder-Verwendung bei Drachen dient in Fig.17 die Photographie eines Drachens, der selbst nicht in Tetraederform ist, sondern nur die Zellen, aus denen er aufgebaut ist.  Dieser Drachen, obwohl er völlig unterschiedlich in Aufbau und Aussehen wie der Aerodrome von Prof. Langley (den ich ein paar Jahre zuvor erfolgreich über dem Potomac fliegen sah) gebaut ist, erinnert trotzdem an den Aerodrom, und es war tatsächlich auch Professor Langley's Apparat, der mich zu diesem Konzept inspiriert hat.
Dieser Drachen, obwohl er völlig unterschiedlich in Aufbau und Aussehen wie der Aerodrome von Prof. Langley (den ich ein paar Jahre zuvor erfolgreich über dem Potomac fliegen sah) gebaut ist, erinnert trotzdem an den Aerodrom, und es war tatsächlich auch Professor Langley's Apparat, der mich zu diesem Konzept inspiriert hat.Die Flügel bestehen hier aus horizontalen zu den Enden hin schief zulaufenden Flächen. Der Grundkörper hat Bootsform, während der Aufbau die Flügelenden jeweils an zwei Punkten in der Nähe von Bug und Heck stützt. Die Tragflächen selbst bestehen ähnlich wie bei einer Libelle aus zwei paar Flügeln. Das ganze Gerüst von Boot und Flügel besteht aus Tetraeder-Zellen, die einen gleichseitigen Tetraeder formen (mit Ausnahme der Diagonalspreizen am Boden des Aufbaus). Der Drachen ist leicht und stabil mit guten Flugeigenschaften. Ich habe diesen Drachen in einer leichten Brise geflogen, indem ich ihn mittels eines Hanfseiles an ein galoppierendes Pferd gebunden habe. Durch Loslassen des Seiles sank der Drachen so vorsichtig, daß während der Landung keinerlei Beschädigungen auftraten.  Fig.20 zeigt eine Modifikation des selben Drachens, in welcher zusätzlich zum Zentralboot noch zwei Seitenflöße befestigt waren, damit der Drachen auf dem Wasser ohne Umkippen schwimmen konnte.
Ein Versuch endete fast in einer Katastrophe, als der Drachen während einer guten Segelbrise einen Windstoß vor dem Start mitbekam. Der Drachen stieg auf und zog die zwei Männer, die ihn halten sollten, mit hinauf. Natürlich ließen sie sofort los, der Drachen stieg beständig auf, bis die Flugschnur, ein Hanfseil mit 1cm Durchmesser, einen Flugwinkel von ca. 45° bildete und dann knallend riß.
Starke Schwingungen mit Pendelcharakter ergaben sich; aber der Drachen befand sich in einer solchen Höhe, als der Unfall passierte, daß die Schwingungen nachließen, bevor noch der Drachen den Boden erreichte. Der Drachen landete sicher und unversehrt auf seinen Kielen auf einem angrenzendem Feld.
Drachen diesen Typs haben eine sehr viele größere Hebekraft, als man zunächst vermuten würde. Die erste Annahme wäre, daß der Auftrieb allein durch die Flügelstruktur bewirkt würde und daß Boot und Seitenflöße nur Gewicht und Luftwiderstand erhöhen würden.
Fig.20 zeigt eine Modifikation des selben Drachens, in welcher zusätzlich zum Zentralboot noch zwei Seitenflöße befestigt waren, damit der Drachen auf dem Wasser ohne Umkippen schwimmen konnte.
Ein Versuch endete fast in einer Katastrophe, als der Drachen während einer guten Segelbrise einen Windstoß vor dem Start mitbekam. Der Drachen stieg auf und zog die zwei Männer, die ihn halten sollten, mit hinauf. Natürlich ließen sie sofort los, der Drachen stieg beständig auf, bis die Flugschnur, ein Hanfseil mit 1cm Durchmesser, einen Flugwinkel von ca. 45° bildete und dann knallend riß.
Starke Schwingungen mit Pendelcharakter ergaben sich; aber der Drachen befand sich in einer solchen Höhe, als der Unfall passierte, daß die Schwingungen nachließen, bevor noch der Drachen den Boden erreichte. Der Drachen landete sicher und unversehrt auf seinen Kielen auf einem angrenzendem Feld.
Drachen diesen Typs haben eine sehr viele größere Hebekraft, als man zunächst vermuten würde. Die erste Annahme wäre, daß der Auftrieb allein durch die Flügelstruktur bewirkt würde und daß Boot und Seitenflöße nur Gewicht und Luftwiderstand erhöhen würden.Dies ist aber bei weitem nicht der Fall. Bootförmige Körper, die einen V-förmigen Querschnitt haben, sind flugfähig und bieten erhebliche Flächen dem Wind dar. Ich habe ein Boot dieser Art ohne jeglichen Flügelaufbau erfolgreich geflogen, und, obwohl es nicht sehr gut flog, hat es sich jedenfalls in der Luft gehalten. Damit war bewiesen, daß das Boot ein wichtiges flugunterstützendes Element der Verbundstruktur ähnlich denen in Fig.17 und 20 ist. Natürlich ist die Anwendung von Tetraeder-Zellen nicht auf Drachen und Flugapparate begrenzt. Sie sind für alle denkbaren Strukturen, wo es auf Stärke und wenig Gewicht ankommt, geeignet. So wie wir Häuser aller Art aus Ziegeln bauen können, so können wir Strukturen aller Art aus Tetraedern bauen, und die Strukturen können so ausgelegt werden, daß sie die selben Merkmale von Gewicht und Festigkeit wie die Einzelzellen besitzen. Ich selbst habe aus diesen Elementen schon ein Haus gebaut, ein Gerüst für einen riesigen Windschutz, drei oder vier Boote und zahlreiche Drachen. Es ist nicht mein Anliegen in diesem Aufsatz, meine Versuche in meinem Labor in Nova Scotia zu beschreiben, sondern einfach Ihnen die Bedeutung von Tetraederstrukturen im Drachenbau näherzubringen. |
© 2000 Thomas-Michael Rudolph